Mente

algorithms.htm

Notes on Algorithms

Algorithms: method for solving a problem.

Data structure: method to store information.

Algorithms + Data Structures = Programs

Background: Type of Algorithms

Lazy Algorithms:

Greedy Algorithms:

Eager Algorithms:

Week 1: Quick Union

Steps to develop a usable algorithm:

  1. Model the problem
  2. Find an algorithm to solve it
  3. Fast enought / fits in memory?
  4. If not, figure out why
  5. Find a way to address the problem
  6. Iterate until satisfied

Dynamic Connectivity

Is there a path between two objects? Used in many applications. The union-find is a problem of maintaining a collection of disjoint sets and performing two operations.

We need to implement: find query and union command.

Find query: check if two objects are in the same component. Union: replace components with their union.

We need to check our API design before implementing it.

Quick Find (eager approach):

Cost model: numer of array accesses.

Find: check if p and q have the same id.

Union: to merge components containing p and q, change all entries whose id equals id[p] to id[q].

Quick Union (lazy approach):

Find: check if p and q have the same root.

Union: to merge components containing p and q, set the id of p's root to the id of q's root.

Quick-find: union too expensive. Trees are flat.

Quick-union: trees can get tall. Find too expensive (could be N array accesses).

Improvements

Weighted quick-union

In sumamry, we try to avoid tall trees as we iterate through the array.

weighted tree comparison


class QuickUnion:
    def __init__(self, n):
        self.id = [i for i in range(n)]
        self.sz = [1 for i in range(n)]

    def root(self, i):
        while i != self.id[i]:
            i = self.id[i]
        return i

    def connected(self, p, q):
        return self.root(p) == self.root(q)

    def union(self, p, q):
        i = self.root(p)
        j = self.root(q)
        self.id[i] = j

    def weighted_union(self, p, q):
        i = self.root(p)
        j = self.root(q)
        if i == j:
            return
        if self.sz[i] < self.sz[j]:
            self.id[i] = j
            self.sz[j] += self.sz[i]
        else:
            self.id[j] = i
            self.sz[i] += self.sz[j]

Running time:

Depth of any node x is at most lg N.

Union-Find Applications

Percolation

N by N grid sites. A system percolates iff top and botom are connected by open sites.

Can be thought of as water flowing through surfaces. Or in Social networks if we want to know whether people are connected.

The subtext of the problem is:

Week 2: Analysis of Algorithms

The key is running time; we used to have a cranking machine; how many cranks we need to do to compute.

Why analyze algorithms?

One of the most important ones is the FFT algorithm; takes only $N log N$ steps. Another one is the N-body simulation.

We use the scientific method to analyze algorithms: Observe, hypothesize, predict, verify, and validate.

Experiments must be reproducible and falsifiable.

3-Sum Example

How many distinct integers add up to zero.

Brute force: do a triple for loop. (it will take n^3)

Mathematical models of runtime

Donald Knuth first proposed the total run-time when programs were running for too long.

E.g., how many instructions as a function of input size N?

Turing said we should just count the most expensive operations instead of each addition.

By focusing on one operation you can simplify the frequency counts.

Order of growth classifications

Small set of functions: log N, N, NlogN, N^2, N^3, 2^N

Alt text

Based on binary search we can find a better algorithm for 3-Sum. We can use N^2 log N instead of N^3.

Instructions:

Types of analysis

We have best case, worst case, and average case. Lower bound on cost, upper bound on cost, and expected cost.

We can have different approaches:

  1. Design for worst case
  2. Randomize the input

The main approach is to reduce variability by focusing on the worst case scenario. We want to find an optimal algorithm.

We have many notations

Example:

The approach:

We can also have tilde notation. It's used to provide an approximate model.

Memory

Typical memory usage for primitive types:

Typical memory usage for objects in Java:

Week 2: Stacks and Queues

Stacks and queues

Stacks

pop()
String item = first.item;
first = first.next;

push()
Node oldfirst = first;
first = new Node();
first.item = "not";
first.next= oldfirst

Alternative Implementation

We have to worry about loitering in Java. To avoid that we need to set the removed item to Null so it can be reclaimed by the garbage collector.

Resizing arrays implementations

Q: How can we grow the array? A: If the array is full, create a new array of twice the size and copy the items. ~3N.

Q: How to shrink array? A: Wait until the array is one-quarter full. Invariant; if the array is always between 25% and 100%

The worst case for push and pop will be N.

Memory: It uses between 8N and 32N.

Tradeoffs

Queues

LinkedList

enqueue()

String item = first.item;
first = first.next;
return item;

dequeue()

Node oldlast = last;
Node last = new Node();
last.item ="not";
last.next = null;

oldlast.next = last;

Generics

We have implemented stacks of strings, but what about URLs, Ints, Vans...

We use the generic type name in Java <Item>

Java doesn't allow generic array creation. We need to create an array of Objects and pass it to a list of items.

s = (Item[]) new Object([Capacity])

Q: What to do about primitive types?

Wrapper type: each primitive type has a wrapper object type. Integer is a wrapper type for int.

Iteration

Design challenge: How can we support iteration over stack items by items.

An Iterable is a method that returns an Iterator. It has methods hasNext() and next()

Why make data structures Iterable? It can helps us write elegant code. Allows us to use for each statements

Week 2: Self Questions

Week 2: Sorting

Q: How does Sort knows how to sort Doubles, Strings, and files without any information?

The sort implementation takes a Comparable[] object. Then call the .compareTo() code.

Yes, you're right. Let's break down the definitions for each of these properties in the context of a binary relation ( $\leq$ ) on a set ( S ):

  1. Antisymmetry:

    • This means that two distinct elements cannot both be "less than or equal to" each other. If they are, they must actually be the same element.

  2. Transitivity:

    • This captures the intuitive idea that if ( a ) is "less than or equal to" ( b ) and ( b ) is "less than or equal to" ( c ), then ( a ) should also be "less than or equal to" ( c ).

  3. Totality (or Completeness):

    • This means that given any two elements in the set, one must be "less than or equal to" the other or vice-versa. This ensures that there are no two elements which can't be compared in the order.

Ex standard order for natural and real numbers, alphabetical orders, chronological orders.

Comparable API

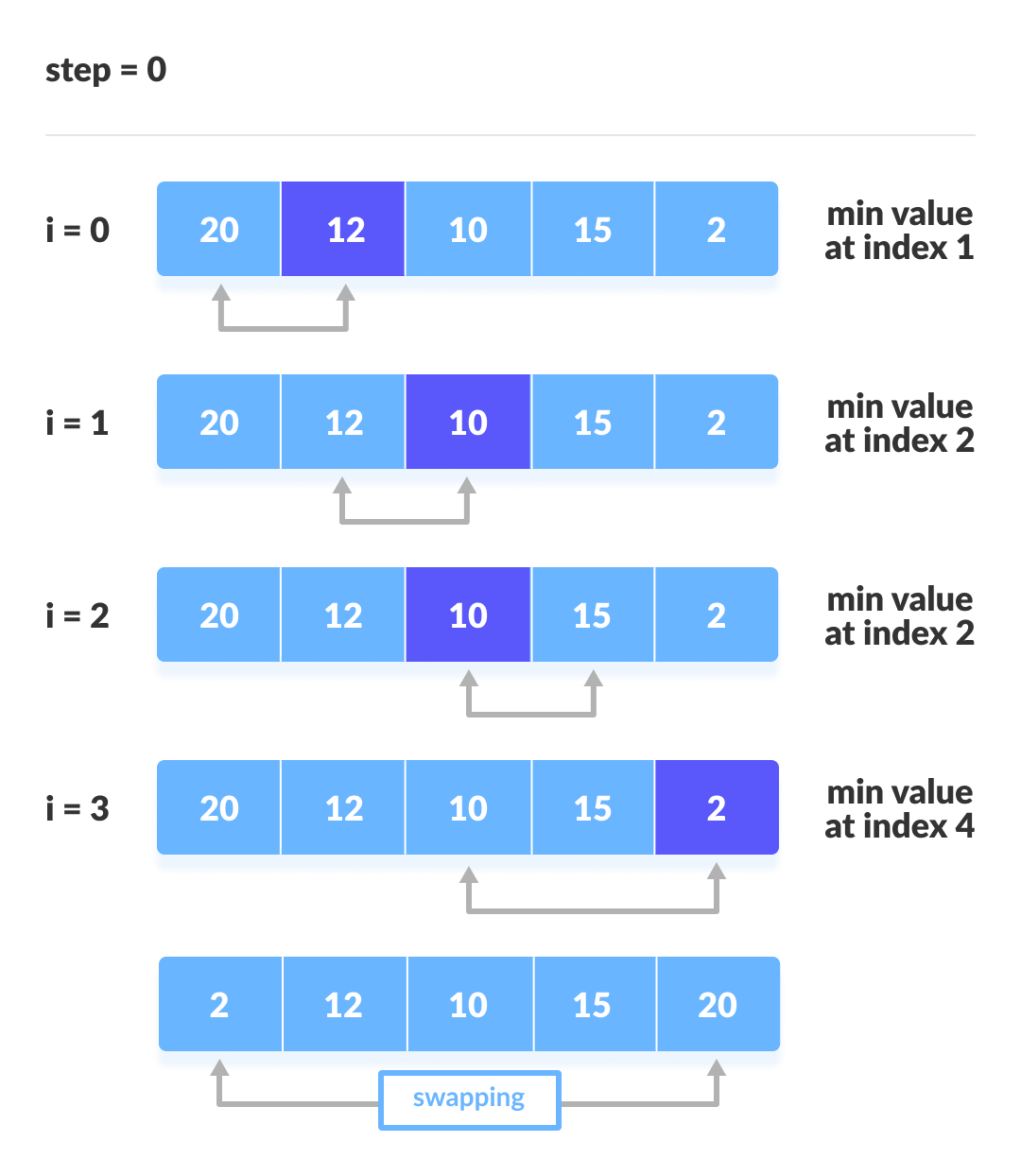
Selection Sort

In iteration I, find index min of smallest remaining entry; swap a[I] and a[min]

Algorithm: scans from left to right.

Selection sort uses $~N^2/2$ compares. It takes quadratic time, even if the input is sorted.

Insertion Sort

In iteration I we swap a[i] with each larger entry to its left.

To sort a randomly ordered arra with distinct keys, it uses $~1/4 N^2$ compares and $~1/4N^2$ exchanges.

If the array is in reverse order, it has to go all the way back to the beginning; if it's in ascending order, it takes 0 exchanges.

For partially sorted arrays, it takes linear time. An array is partially sorted if the number of inversions is less than some constant cN.

insertion sort

Shellsort

Move entries more than one position at a time by h-sorting the array. An h-sorted array is h interleaved sorted subsequences. (1959 sorting method)

H-sort is just insertion sort with stride length h. Why do this?

Which increment sequence to use?

The worst case number of compares used by shell sort is $O(N^(3/2))$

Shell sort is a simple idea leading to substantial performance gains. It involves very little code, used often in hardware (embedded systems)

shell sort

Shuffle sort

Knuth sort: in iteration I, pick integer r between 0 and I uniformly at random. Then we swap a[I] and a[r].

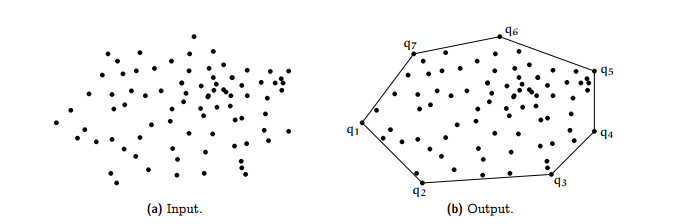
Convex Hull

The convex hull of a set of N points is the smallest perimeter fence enclosing the points.

E.g.,

Graham scan demo

Week 3: Self-Questions

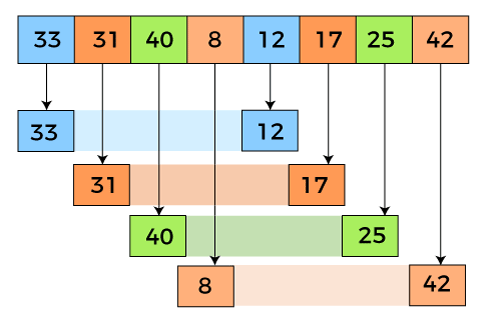
Week 3: Merge Sort

Copy to an auxiliary array. ** 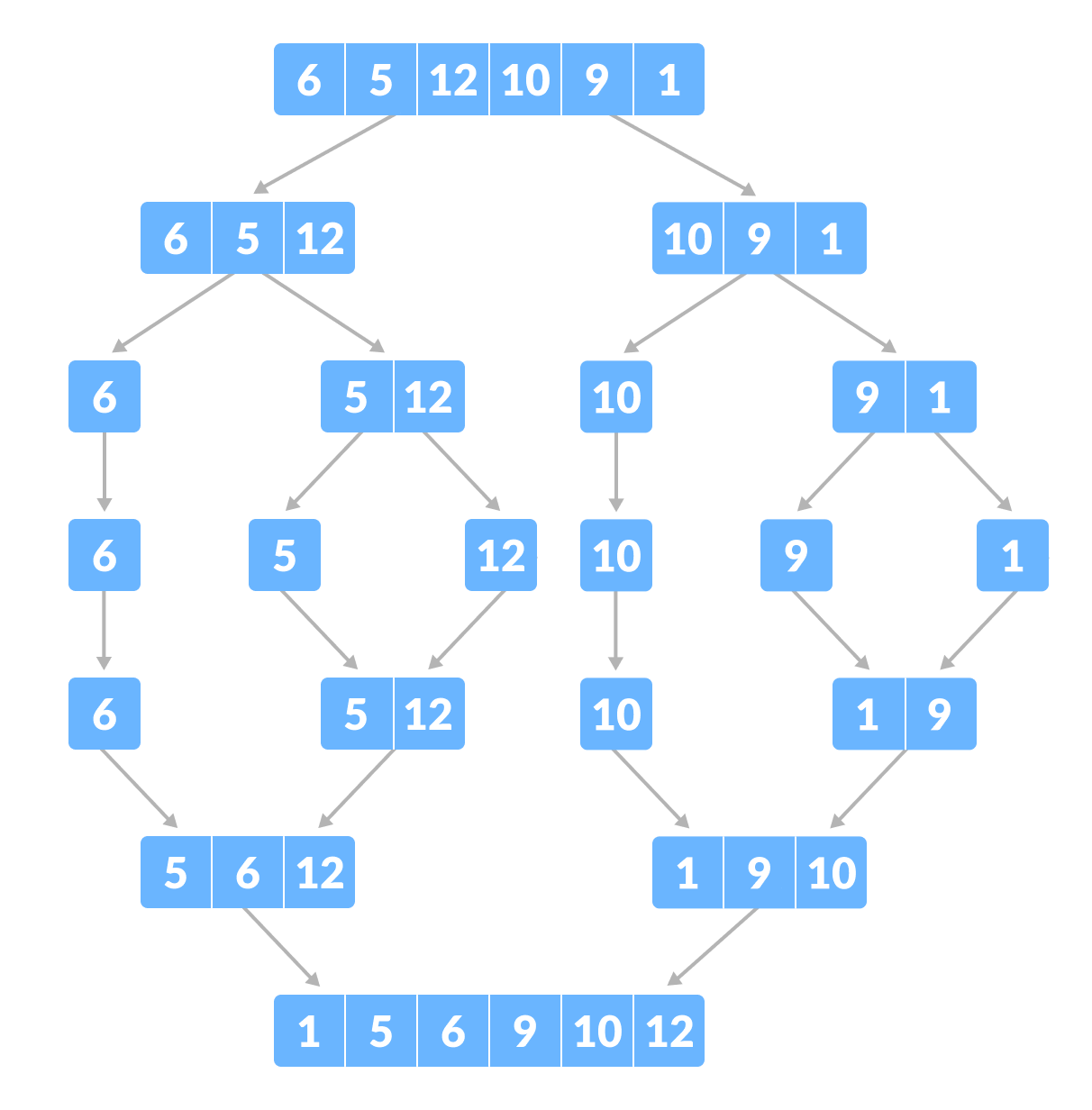mergesort

Mergesort uses at most NlgN compares and 6NlgN array accesses to sort any array of size N.

Mergesort uses extra space proportions to N.

Practical improvements:

# split in half
m = n / 2

# recursive sorts
sort a[1..m]
sort a[m+1..n]

# merge sorted sub-arrays using temp array
b = copy of a[1..m]
i = 1, j = m+1, k = 1
while i <= m and j <= n,
    a[k++] = (a[j] < b[i]) ? a[j++] : b[i++]
    → invariant: a[1..k] in final position
while i <= m,
    a[k++] = b[i++]
    → invariant: a[1..k] in final position

Bottom-up Merge Sort (no recursion)

Basic plan

Sorting Complexity

Computational complexity: framework to study efficiency of algorithms to solve problem X.

E.g. Sorting

Comparators

We also have a comparator interface to sort using an alternate order.

int compare(Key v, Key w)

E.g.,

Arrays.sort(a, Student.BY_NAME)
Arrays.sort(points, p.POLAR_ORDER)

Stability

A typical application: first sort by name, then by section.

A stable sort is one that presents the same order of items with a given key.

Insertion sort and merge sort are stable (but not selection sort or shell sort)

We can move items past items that are equal.

Self Questions

Week 3: Quick-sort

Basic Plan:

Summary:

Implementation details:

Performance:

Properties:

Week 3: Selection Sort

Goal: Given an array of N items, find the Kth largest. i.e., return the top K.

Quick Select:

3-Way Quick sort (Dijkstra Implementation)

Week 3: Applications

Each sort type will have different attributes:

System sorts cannot possibly cover all possible algorithms.

Week 3: Self Questions

Week 4

Priority Queues API

Collections:

Applications:

Implementation:

The binary heap comes from a complete binary tree. Perfectly balanced except for the bottom level.

Heap-ordered binary tree

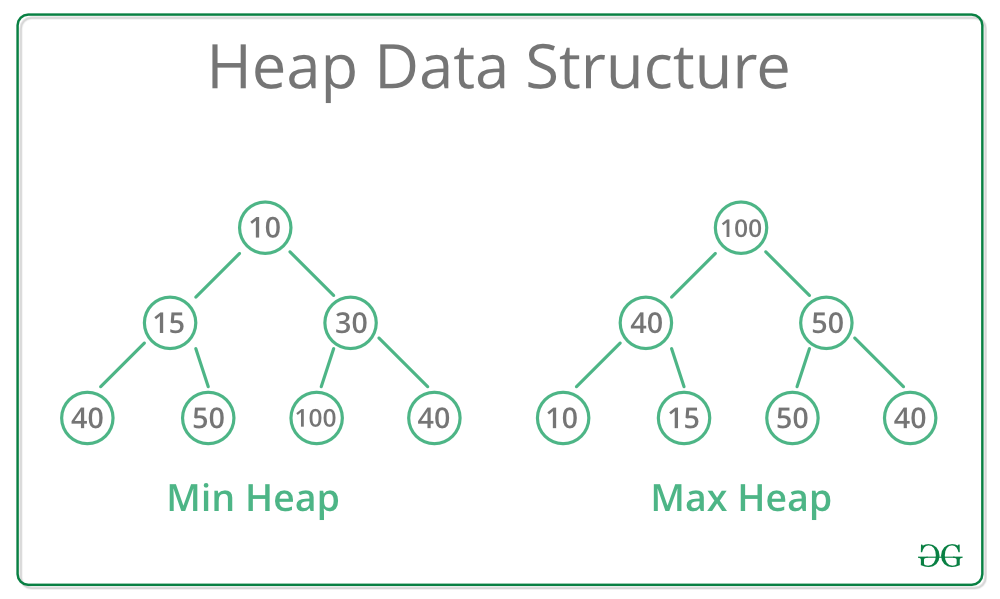
https://media.geeksforgeeks.org/wp-content/cdn-uploads/20221220165711/MinHeapAndMaxHeap1.png

If we insert a key larger than its parents we exchange them until the order is restored.

To insert into a heap, we add a node at the end then swim it up with at most 1 + lg N compares. AKA Peter principle; promoted to level of incompetence.

If the parent's key becomes smaller than one or both, we figure out which children is higher then exchange them until the order is restored (recursively). AKA better subordinate promoted (power struggle)

To delete the maximum, we exchange root with node at end, then sink it down. At most 2 Log N compares.

Considerations:

Java Note on Immutability: when we use final those values can't change once created.

Immutable: String, Integer, Double, Color, Vector, Transaction...

Why use?

We should make classes immutable as much as possible - Creator of Java

Week 3: Heapsort

Complexity

Significance: In-place sorting algorithm with NlogN worst-case.

Week 4: Symbol Tables

DNS lookup

API Examples

We associate one value with each key.

Conventions:

Value type: any generic type.

Best practices - use immutable types for symbol table keys.

All Java classes inherit a method equals()

Symbol Table Implementations

Sequential Search (Unordered LinkedList)

We use a LinkedList in this implementation.

Binary search in an ordered array

Ordered Operations

We can add more operations to a Symbol Table such as:

We normally argue against wide interfaces.

Binary Search Trees

A BST is a binary tree in symmetric order.

It is either:

Each node has a key and every node's key is:


private class Node
    /